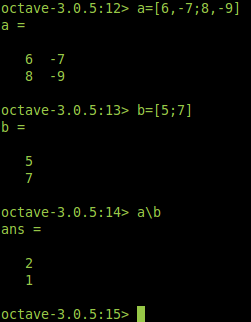
Para la resolución de sistemas de ecuaciones del tipo Ax = b se utiliza la notación a\b. Por ejemplo, para calcular el siguiente sistema de ecuaciones de primer grado con dos incógnitas,
6·x - 7·y = 5
8·x - 9·y = 7
se procede de la manera siguiente: se guardan los elementos x e y en una matriz a y la igualdad en un vector b, y finalmente se ejecuta el comando a\b.
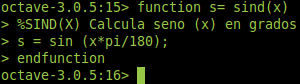
En Octave es posible crear funciones propias, escribirlas directamente desde la línea de comandos o ejecutarlas desde un archivo externo.
Las funciones creadas desde la línea de comandos deben cumplir con el siguiente formato:
function variable_salida = nombre_funcion (argumentos_entrada)
cuerpo _funcion
endfunction
En caso de devolver varias variables, éstas deben estar encerradas entre corchetes.
function [salida1,salida2]...
Para que Octave ejecute un archivo éste debe tener extensión '.m' y debe encontrarse en el directorio desde donde se ejecute Octave. También es posible agregar rutas adicionales con el comando addpath('ruta'), donde 'ruta' es el camino al directorio que contiene los scripts. Para borrar la ruta usamos rmpath('ruta').
La forma más simple para producir gráficas bidimensionales en Octave se hace a través del comando plot(x[,y][,fmt]), donde 'x', y opcionalmente 'y', representan los vectores coordenadas para cada punto, adicionalmente se puede especificar una serie de formatos que cambiarán la apariencia de salida de la gráfica, esto incluye el estilo de línea, el color y otras características.
A continuación se presentan los diferentes argumentos que podemos usar para modificar el formato de la gráfica, se puede usar tanto comillas simples (') como dobles (“).
Tabla 62.2. Algunas de las opciones para la generación de gráficas en Octave:
| Signo | Descripción |
|---|---|
| '' | Une los datos mediante segmentos de línea (opción por defecto). |
| '. ' | Asigna un punto a cada dato. |
| '@ ' | Asigna un punto grande para cada dato. |
| '@ ' | Une los puntos (grandes) de cada dato con segmentos de línea. |
| '^ ' | Gráfica estilo impulso (línea que va desde cero hasta el punto). |
| 'L ' | Gráfica tipo escalera. |
| '# ' | Diagrama de cajas. |
| 'n ' | Asigna un color a los datos, donde n es un dígito del 0 al 9 que representa el color. |
| 'nm ' | Asigna un color y un estilo de punto , donde n y m son dígitos del 0 al 9, n representa un color y m el estilo del punto. |
El argumento 'fmt' puede también ser usado para asignarle una etiqueta a los datos, para ello se coloca la etiqueta inmediatamente después del argumento, hay que asegurarse de colocar el texto entre punto y coma (;) antes de cerrar con la comilla.
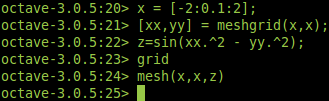
Para producir gráficos en 3D disponemos de varias opciones, la mas simple es usar el comando plot3(x,y,z) donde cada argumento es tomado para convertirse en los vértices del gráfico tridimensional.
Si todos los argumentos son vectores de la misma longitud se dibujará una única línea continua. Si todos los argumento son matrices cada una de las columnas de las matrices serán tratada como líneas separadas.
El comando mesh(x,y,z) hace una representación tridimensional dados dos vectores 'x' e 'y', y una matriz bidimensional 'z'. Generalmente se usa el comando meshgrid para generar los datos que usará mesh para representar los ejes 'x' e 'y'.
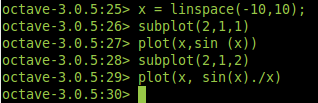
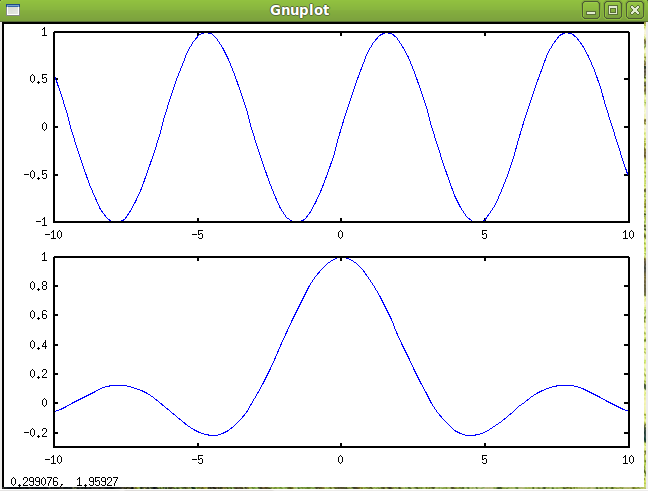
En Octave es posible mostrar diferentes gráficos en una misma ventana, para ello se usa la función subplot(filas, columnas, indice). El comando subplot divide la ventana de gráficos en un conjunto de ventanas más pequeñas. El argumento indice específica el la ventana actual dentro del arreglo.
El índice se desplaza primero por cada ventana dentro de una fila para luego pasar a la otra, de izquierda a derecha y desde arriba hacia abajo.